Нуль-тест с зеркальным компенсатором для проверки параболических зеркал

Sky and Telescope 1992 № 07

Автор: Эд Джонс

Под редакцией Роджера В. Синнотта

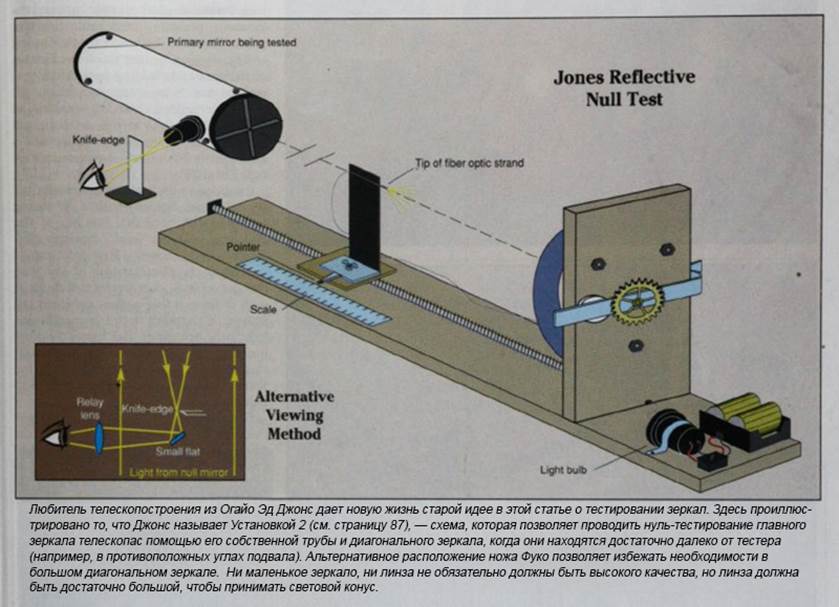
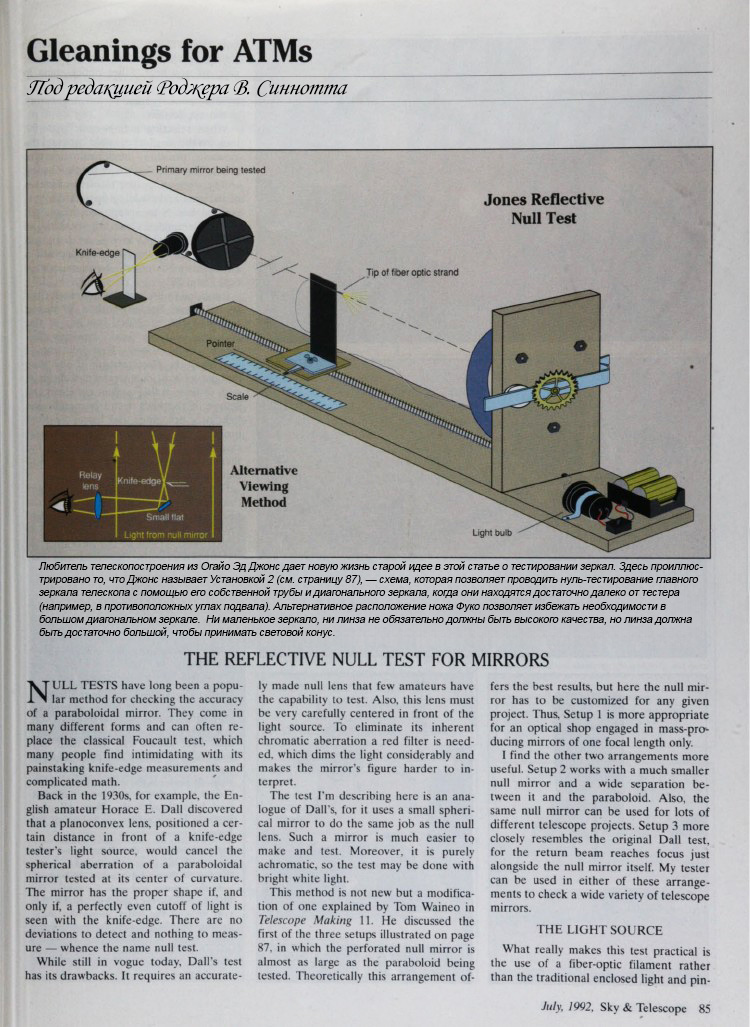
Введение в метод нуль-тестирования

Нуль-тесты уже давно зарекомендовали себя как популярный и эффективный метод проверки точности параболических зеркал. Они существуют в различных модификациях и во многих случаях могут успешно заменить классический тест Фуко, который часто вызывает затруднения у начинающих оптиков из-за необходимости проведения кропотливых измерений продольных аберраций с помощью теневого прибора и последующих сложных математических расчётов допусков.

Историческая справка: открытие Долла

В 1930-х годах английский астроном-любитель Гораций Э. Долл сделал важное открытие. Он обнаружил, что плоско-выпуклая линза, размещённая на определённом расстоянии перед источником света теневого прибора, способна компенсировать сферическую аберрацию параболического зеркала, когда оно тестируется в своём центре кривизны. Суть метода заключается в том, что правильно сформированное параболическое зеркало при использовании ножа теневого прибора даёт идеально равномерное затемнение светового пучка без видимых отклонений. Это исключает необходимость проведения каких-либо измерений - отсюда и происходит название "нуль-тест".

Ограничения классического теста Долла

Несмотря на свою популярность, тест Долла имеет несколько существенных недостатков:

1. Требуется изготовление высокоточных эталонных линз, качество которых могут проверить лишь немногие опытные оптики.

2. Линза должна быть идеально отцентрирована относительно источника света, что требует дополнительных юстировочных приспособлений.

3. Присущая линзам хроматическая аберрация вынуждает использовать красный светофильтр, что значительно снижает яркость изображения и затрудняет визуальную оценку поверхности зеркала.

Зеркальный компенсатор: принцип работы

Предлагаемый мной модифицированный тест является аналогом теста Долла, но вместо линзы использует небольшое сферическое зеркало в качестве компенсатора. Такое решение имеет несколько принципиальных преимуществ:

• Сферические зеркала значительно проще изготовить и проверить на точность по сравнению с линзами.

• Зеркальный компенсатор полностью свободен от хроматических аберраций, что позволяет проводить тестирование при ярком белом освещении.

• Один и тот же компенсатор может использоваться для проверки зеркал с разными параметрами.

Конфигурации тестовых установок

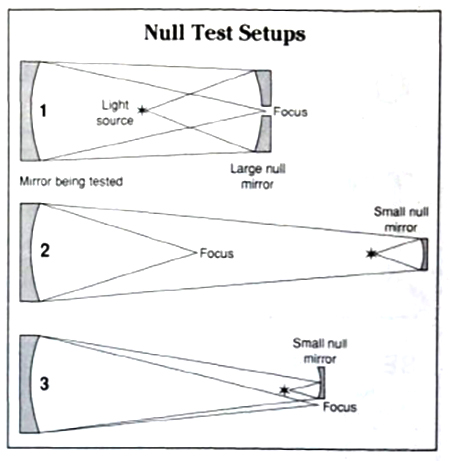
Том Вайнео в журнале "Telescope Making" (выпуск 11) описал три возможные схемы расположения компенсатора:

Установка 1: Эталонное зеркало с центральным отверстием

В этой конфигурации используется сферическое зеркало, по размеру близкое к тестируемому параболоиду и имеющее центральное отверстие. Хотя теоретически такая схема даёт наилучшие результаты, на практике она неудобна, так как требует изготовления индивидуального компенсатора для каждого конкретного зеркала. Поэтому Установка 1 в основном применяется в оптических мастерских, специализирующихся на серийном производстве зеркал.

Установка 2: Малый компенсатор с большим рабочим расстоянием

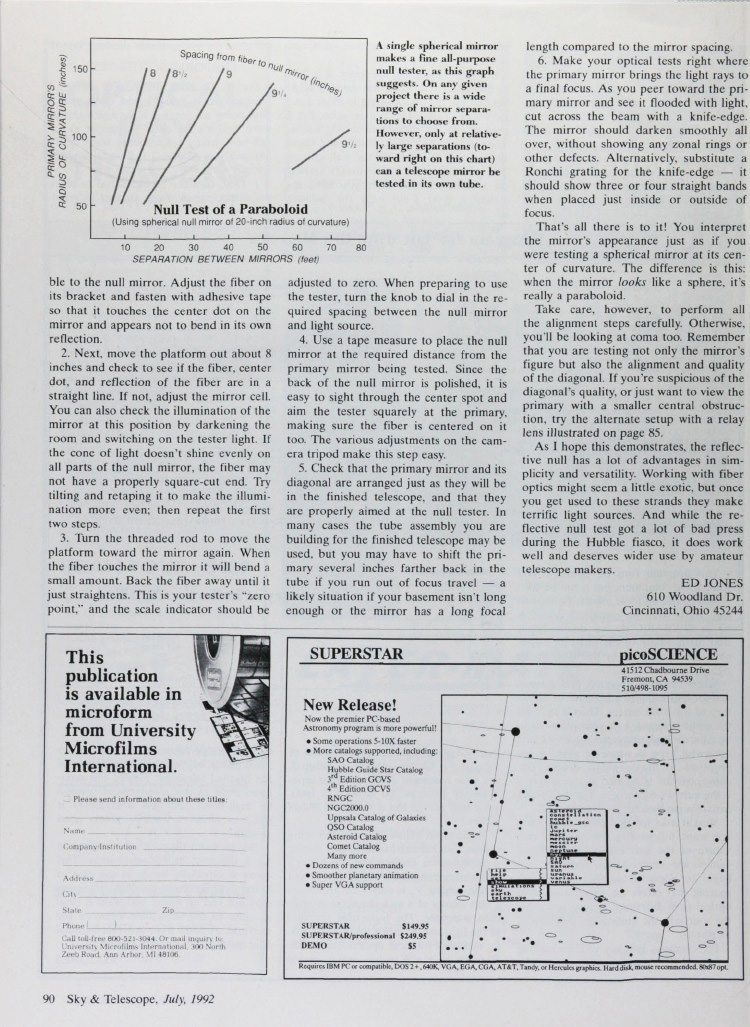
Эта схема предусматривает использование значительно меньшего по размеру компенсатора, расположенного на большем расстоянии от тестируемого зеркала. Главное преимущество - универсальность: один и тот же компенсатор может использоваться для проверки различных зеркал. Именно эту конфигурацию я рекомендую для большинства любительских применений.

Установка 3: Фокусировка пучка у компенсатора

Эта схема наиболее близка к оригинальному тесту Долла, так как возвращающийся пучок света фокусируется вблизи самого компенсатора. Хотя она также работоспособна, я советую сначала освоить Установку 2 как более простую в настройке.

Конструкция источника освещения

Ключевым элементом, сделавшим этот тест практичным для любителей, стало использование волоконно-оптического световода вместо традиционного закрытого источника с точечным отверстием. Поскольку источник должен располагаться внутри светового конуса и быть предельно малым, волоконная оптика оказалась идеальным решением.

Выбор оптического волокна

Волоконная оптика бывает нескольких типов:

• По материалу: пластиковая или стеклянная

• По режиму передачи: одномодовая или многомодовая

Для наших целей важно выбрать волокно с:

1. Минимально возможным диаметром сердцевины (я использовал 50 микрон)

2. Максимальной числовой апертурой (NA)

Числовая апертура, определяемая соотношением коэффициентов преломления сердцевины и оболочки, характеризует способность волокна собирать свет. Например:

• NA=0.17 соответствует углу приёма около 20° (свет не может войти или выйти из волокна за пределами конуса в 20°

• NA=0.42 позволяет принимать свет под углом до 50°

Я остановил свой выбор на многомодовом стеклянном волокне марки Belden с NA=0.200.

Изготовление источника света

1. Снимите пластиковую оболочку с волоконного пучка

2. Аккуратно выделите отдельную нить

3. Проверьте качество торцевого среза - он должен быть строго перпендикулярен оси

4. Для освещения использовал галогеновую лампу на 3В, закрепив волокно эпоксидной смолой

Расчёт параметров тестовой системы

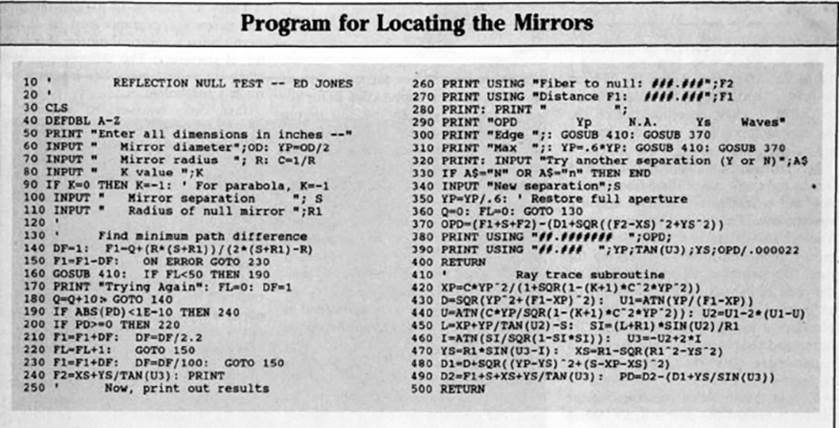
Для точной работы теста критически важно правильно определить взаимное расположение всех компонентов. Сферическое зеркало должно вносить ровно столько сферической аберрации, чтобы полностью компенсировать аберрацию тестируемого параболоида. Следовательно, расстояния между зеркалом и источником света крайне важны. График показывает, насколько универсальным может быть стенд, подобный моему:

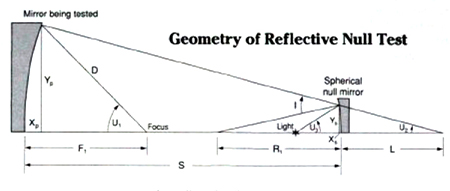
Программное обеспечение для расчётов

Я разработал специализированную программу которая позволяет рассчитать:

1. Оптимальные расстояния между компонентами

2. Используемую часть поверхности компенсатора

3. Точность компенсации в длинах волн

4. Требуемую числовую апертуру волокна

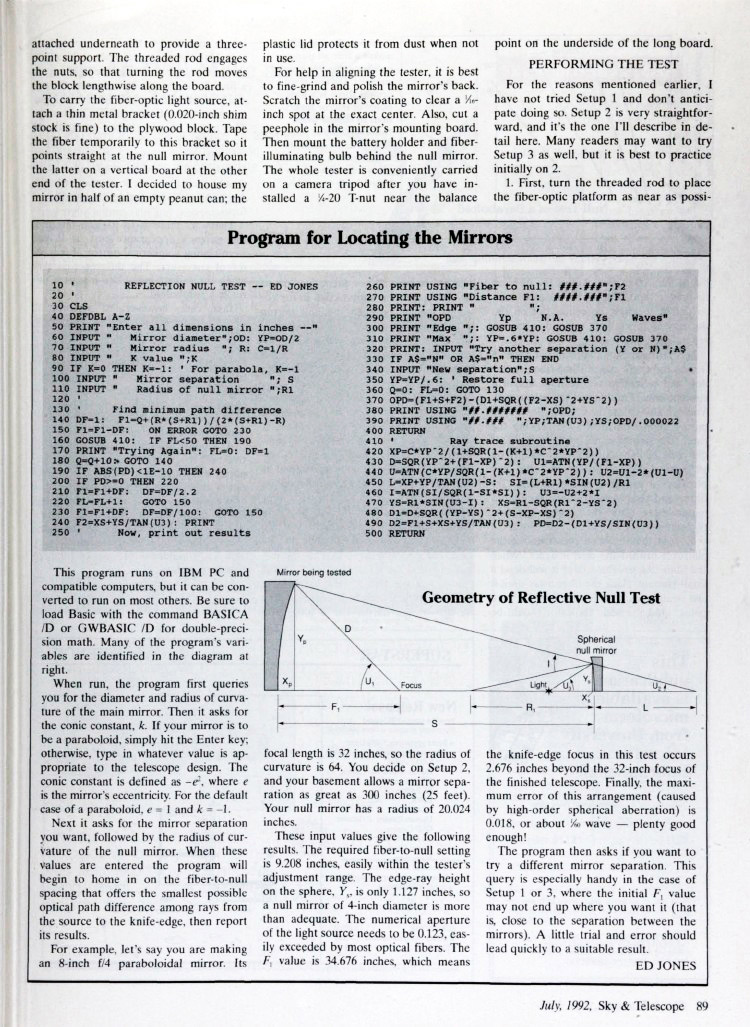
Эта программа работает на IBM PC и совместимых компьютерах, но её можно адаптировать для других систем. Загрузите Basic с командами BASICA JD или OWBASJC JD для вычислений с двойной точностью. Многие переменные программы обозначены на схеме. При запуске программа сначала запрашивает диаметр и радиус кривизны тестируемого зеркала. Затем она спрашивает о конической постоянной. Если ваше зеркало параболическое, просто нажмите Enter; в противном случае введите значение, соответствующее конструкции телескопа. Коническая постоянная определяется как k = −e², где e — эксцентриситет зеркала. Для параболоида по умолчанию e² =1 и k =−1. Далее программа запрашивает желаемое расстояние между зеркалами и радиус кривизны эталонного зеркала. После ввода этих значений программа начнёт подбирать расстояние между оптоволокном и эталонным зеркалом, обеспечивающее минимальную разницу оптического пути лучей от источника до ножа Фуко, и выведет результаты.

Программа работает для всех трёх конфигураций установок и включает все необходимые формулы, приведённые Вайнео.

Пример параметров компенсатора

Допустим, вы делаете 8-дюймовое параболическое зеркало с относительным отверстием f/4. Его фокусное расстояние — 32 дюйма, поэтому радиус кривизны равен 64 дюймам. Вы выбираете Настройку 2, а расстояние между зеркалами в вашей лаборатории может достигать 300 дюймов (25 футов). Радиус кривизны нулевого зеркала — 20024 дюйма.

• Требуемое расстояние между оптоволокном и нулевым зеркалом — 9,208 дюймов (легко регулируется)

• Высота краевого луча на сфере Yn Y n​  — всего 1,47 дюйма, поэтому нулевое зеркало диаметром 4 дюйма более чем достаточно

• Числовая апертура источника света — 0,123 (большинство оптоволокон её превышают)

• Значение FN F N​  — 34,676 дюйма, что означает, что фокус ножа Фуко в этом тесте находится на 2,676 дюйма дальше фокуса готового телескопа (32 дюйма)

• Максимальная погрешность (из-за сферической аберрации высокого порядка) — 0,016, или примерно 1/36 длины волны — вполне допустимо!

Затем программа спрашивает, хотите ли вы изменить расстояние между зеркалами. Это особенно полезно для Настроек 1 или 3, где начальное значение FN F N​ может не соответствовать желаемому (т.е. близкому к расстоянию между зеркалами). Несколько пробных попыток помогут быстро найти подходящий результат.

В моей установке используется:

• Диаметр: 4 дюйма (101.6 мм)

• Радиус кривизны: 20 дюймов (508 мм)

Однако программа позволяет адаптировать систему под  широкий спектр любительских параболических зеркал.

Изготовление тестового стенда

Основные компоненты стенда:

1. Несущая конструкция: 14-дюймовый (355 мм) резьбовой стержень, закреплённый на длинной доске

2. Подвижная платформа: фанерный квадрат с двухгаечным механизмом перемещения

3. Крепление волокна: тонкая металлическая скоба (толщиной 0.020 дюйма)

4. Установка компенсатора: вертикальная доска с держателем зеркала

Юстировочные приспособления

Для удобства настройки:

1. Задняя поверхность компенсатора тщательно отшлифована и отполирована

2. В центре зеркала сделана отметка (процарапано покрытие на диаметре 1/4 дюйма)

3. В монтажной доске просверлено смотровое отверстие

Проведение тестирования

Этап 1: Юстировка компенсатора

1. Установите платформу с волокном вблизи компенсатора

2. Отрегулируйте положение волокна так, чтобы его изображение совпадало с центральной меткой

3. Проверьте равномерность освещения поверхности компенсатора

Этап 2: Определение нулевой точки

1. Медленно приближайте волокно к зеркалу до легкого касания

2. Отодвиньте до положения, где волокно выпрямляется

3. Отметьте это положение как "ноль" на измерительной шкале

Этап 3: Тестирование параболического зеркала

1. Установите компенсатор на расчётном расстоянии от тестируемого зеркала

2. Обеспечьте точную соосность всех компонентов

3. Проведите тест Фуко или используйте решётку Ронки

Критерий правильности формы:

• Для теста Фуко - равномерное затемнение всей поверхности

• Для решётки Ронки - прямые, равномерно расположенные полосы

Заключение и рекомендации

Несмотря на некоторую критику, связанную с проблемами телескопа "Хаббл", зеркальный нуль-тест остаётся мощным и точным методом контроля качества оптических поверхностей. Его основные преимущества:

• Простота интерпретации результатов

• Отсутствие необходимости в сложных измерениях

• Возможность использования одного компенсатора для разных зеркал

• Работа с полным спектром белого света

Для получения наилучших результатов рекомендую:

1. Тщательно проводить все юстировочные процедуры

2. Проверять качество всех оптических компонентов

3. Начинать освоение метода с Установки 2 как наиболее простой

    

Эд Джонс
610 Woodland Drive
Цинциннати, Огайо 45244
США

-------------------------------------------------------------------------------------

Код программы на С под консоль (без тестирования и отладки)     #include <stdio.h> #include <math.h> #include <windows.h> #include <locale.h> struct OpdValues { double pd; double xs; double ys; double u3; double d1; }; struct OpdValues opdCalc(double r1, double f1, double s, double c, double yp, double k); int main() { // Настройка локализации и кодировки setlocale(LC_ALL, "Russian"); SetConsoleOutputCP(CP_UTF8); SetConsoleCP(CP_UTF8); const int bufSize = 130; char inbuf[bufSize]; // Константа для перевода дюймов в мм (1 дюйм = 25.4 мм) const double inchToMm = 25.4; // Значения по умолчанию (переведенные в мм) double od = 8.0 * inchToMm; // 203.2 мм double r = 64.0 * inchToMm; // 1625.6 мм double k = -1.0; // Безразмерный коэффициент double s = 300.0 * inchToMm; // 7620.0 мм double r1 = 20.024 * inchToMm; // 508.6096 мм double yp, c, df, f1, q = 0.0; double pd = 0, last_pd = 0; double f2, opd, ypVar, maxOpd; int fl, opdIndex; // Ввод параметров с подсказками в мм printf("Оптический калькулятор для тестирования зеркал (все значения в мм)\n"); printf("---------------------------------------------------------------\n"); printf("Световой диаметр изделия [%.2f]: ", od); fgets(inbuf, bufSize, stdin); if (sscanf(inbuf, "%lf", &od) != 1) od = 8.0 * inchToMm; yp = od / 2; printf("Радиус кривизны зеркала [%.2f]: ", r); fgets(inbuf, bufSize, stdin); if (sscanf(inbuf, "%lf", &r) != 1) r = 64.0 * inchToMm; c = 1 / r; printf("Коэффициент K (конусность) [%.2f]: ", k); fgets(inbuf, bufSize, stdin); if (sscanf(inbuf, "%lf", &k) != 1) k = -1.0; printf("Расстояние между зеркалами [%.2f]: ", s); fgets(inbuf, bufSize, stdin); if (sscanf(inbuf, "%lf", &s) != 1) s = 300.0 * inchToMm; printf("Радиус нуль-корректора [%.2f]: ", r1); fgets(inbuf, bufSize, stdin); if (sscanf(inbuf, "%lf", &r1) != 1) r1 = 20.024 * inchToMm; // Проверка знаменателя double denom = (2 * (s + r1) - r); while (fabs(denom) < 1e-10) { printf("Ошибка: недопустимое расстояние между зеркалами!\n"); printf("Введите новое расстояние между зеркалами (мм): "); fgets(inbuf, bufSize, stdin); sscanf(inbuf, "%lf", &s); denom = (2 * (s + r1) - r); } // Основной расчет df = 1.0; f1 = q + (r * (s + r1)) / denom; printf("\nВыполняются расчеты...\n"); while (fabs(pd) >= 1e-10) { f1 = f1 - df; for (fl = 1; fl <= 50; fl++) { f1 = f1 - df; struct OpdValues opdResult = opdCalc(r1, f1, s, c, yp, k); pd = opdResult.pd; if (pd == last_pd) fl = 50; if (fabs(pd) > fabs(last_pd)) { f1 = f1 + df; df = -df / 2.0; } last_pd = pd; } q = q + 10.0; } // Финальные расчеты struct OpdValues finalResult = opdCalc(r1, f1, s, c, yp, k); f2 = finalResult.xs + finalResult.ys / tan(finalResult.u3); opd = (f1 + s + f2) - (finalResult.d1 + sqrt(pow(f2 - finalResult.xs, 2) + pow(finalResult.ys, 2))); // Вывод результатов printf("\nРЕЗУЛЬТАТЫ (в мм):\n"); printf("---------------------------------------------------------------\n"); printf("Волокно до нуль-корректора: %12.4f мм\n", f2); printf("Зеркало до тестового фокуса: %12.4f мм\n", f1); printf("Высота краевого луча: %12.4f мм\n", yp); printf("Угол раскрытия (TAN U3): %12.6f\n", tan(finalResult.u3)); printf("Высота луча на тестовом зеркале: %12.4f мм\n", finalResult.ys); printf("OPD на краю: %12.6f длин волн\n", opd / 0.00055); // Расчет максимальной OPD maxOpd = 0.0; for (opdIndex = 1; opdIndex <= 10; opdIndex++) { ypVar = yp * opdIndex / 10; struct OpdValues res = opdCalc(r1, f1, s, c, ypVar, k); f2 = res.xs + res.ys / tan(res.u3); opd = (f1 + s + f2) - (res.d1 + sqrt(pow(f2 - res.xs, 2) + pow(res.ys, 2))); if (opd > maxOpd) maxOpd = opd; } printf("Максимальная OPD: %12.6f длин волн\n", maxOpd / 0.00055); // Данные для OSLO printf("\nДАННЫЕ ДЛЯ OSLO:\n"); printf("---------------------------------------------------------------\n"); printf("Поверхность Радиус (мм) Толщина (мм) Показатель Конусность\n"); printf("OBJ %12.2f %12.2f n/a n/a\n", 0.0, f2); printf("1 %12.2f %12.2f -1.0 0.0\n", -r1, -s); printf("2 %12.2f %12.2f 1.0 %.5f\n", r, f1, k); printf("\nРасчет завершен. Нажмите Enter для выхода..."); fgets(inbuf, bufSize, stdin); return 0; } struct OpdValues opdCalc(double r1, double f1, double s, double c, double yp, double k) { struct OpdValues result; double xp = (c * pow(yp, 2)) / (1 + sqrt(1 - (k + 1) * pow(c * yp, 2))); double d = sqrt(pow(yp, 2) + pow(f1 - xp, 2)); double u1 = atan(yp / (f1 - xp)); double u = atan((c * yp) / sqrt(1 - (k + 1) * pow(c * yp, 2))); double u2 = u1 - 2 * (u1 - u); double l = xp + (yp / tan(u2)) - s; double si = ((l + r1) * sin(u2)) / r1; double i = asin(si); double u3 = -u2 + 2 * i; double ys = r1 * sin(u3 - i); double xs = r1 * (1 - sqrt(1 - pow(ys / r1, 2))); double d1 = d + sqrt(pow(yp - ys, 2) + pow(s - xp - xs, 2)); double d2 = f1 + s + xs + (ys / tan(u3)); result.pd = d2 - (d1 + (ys / sin(u3))); result.xs = xs; result.ys = ys; result.u3 = u3; result.d1 = d1; return result; } Результат расчёта (исходные данные переведены в СИ)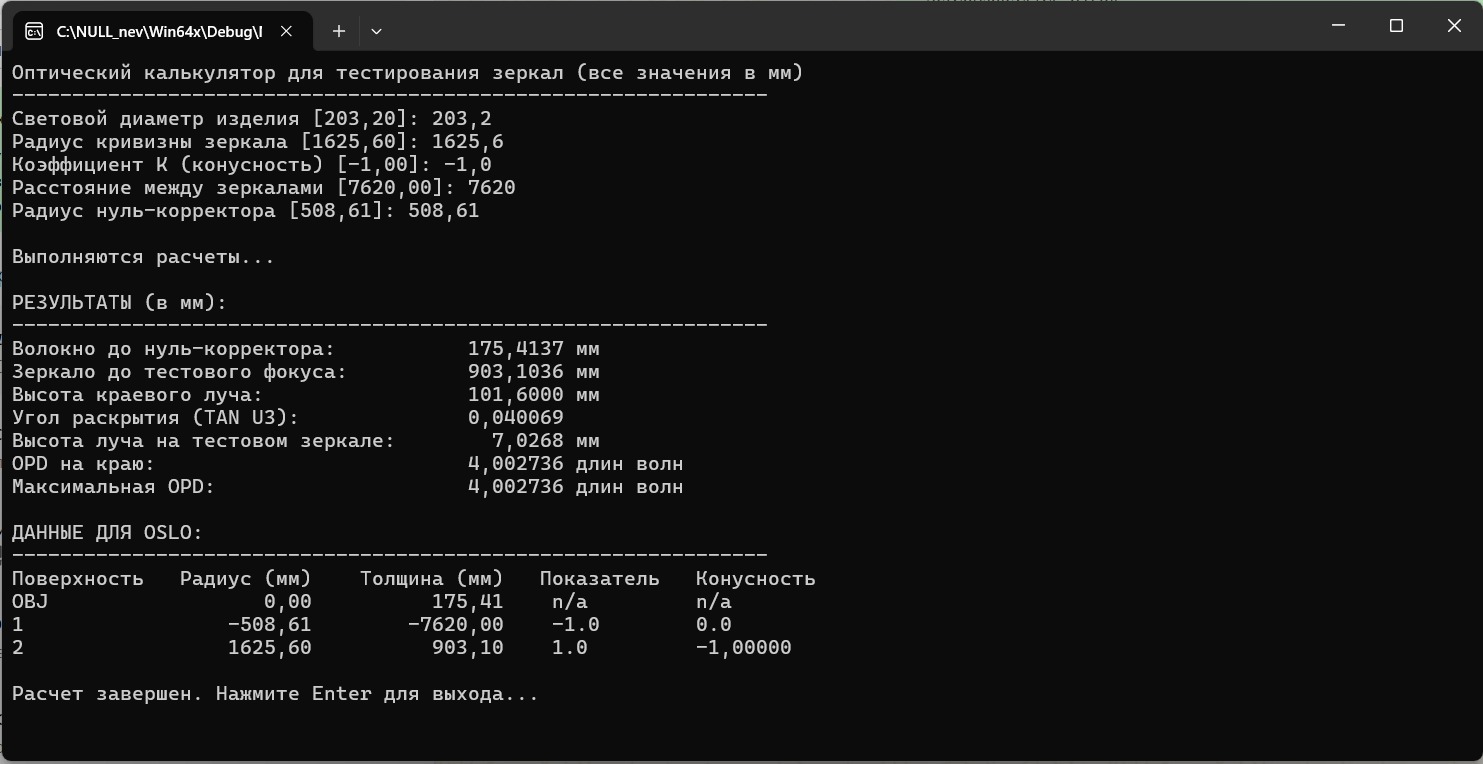

Опубликовано 01.05.2025