Отражательный нуль-тест для параболоидов

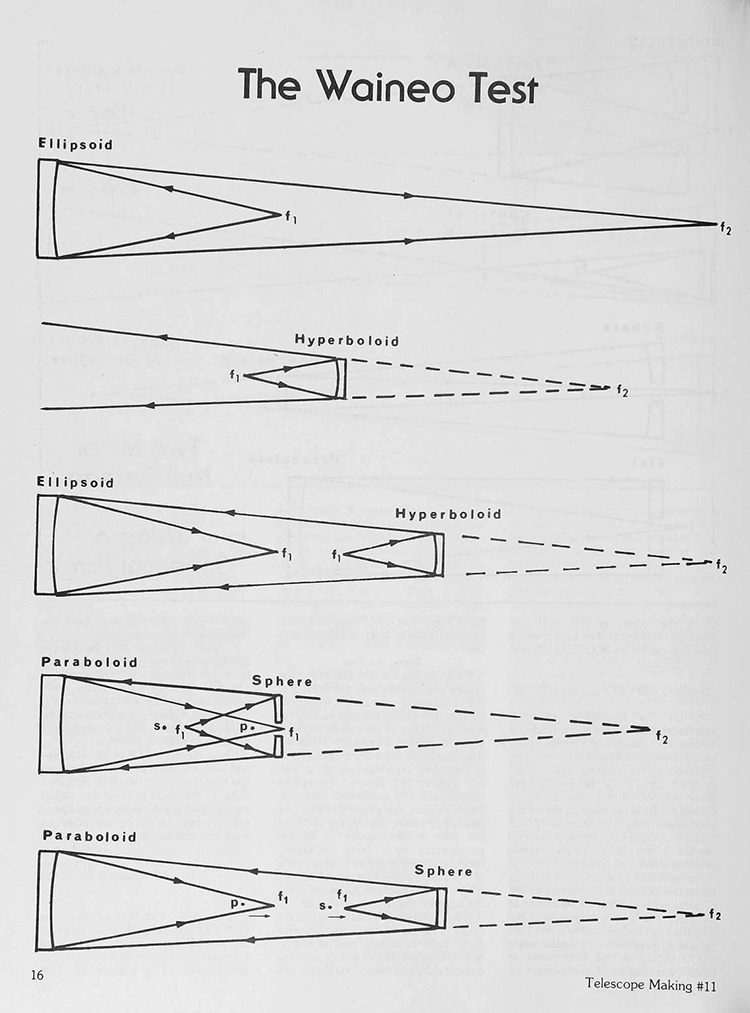
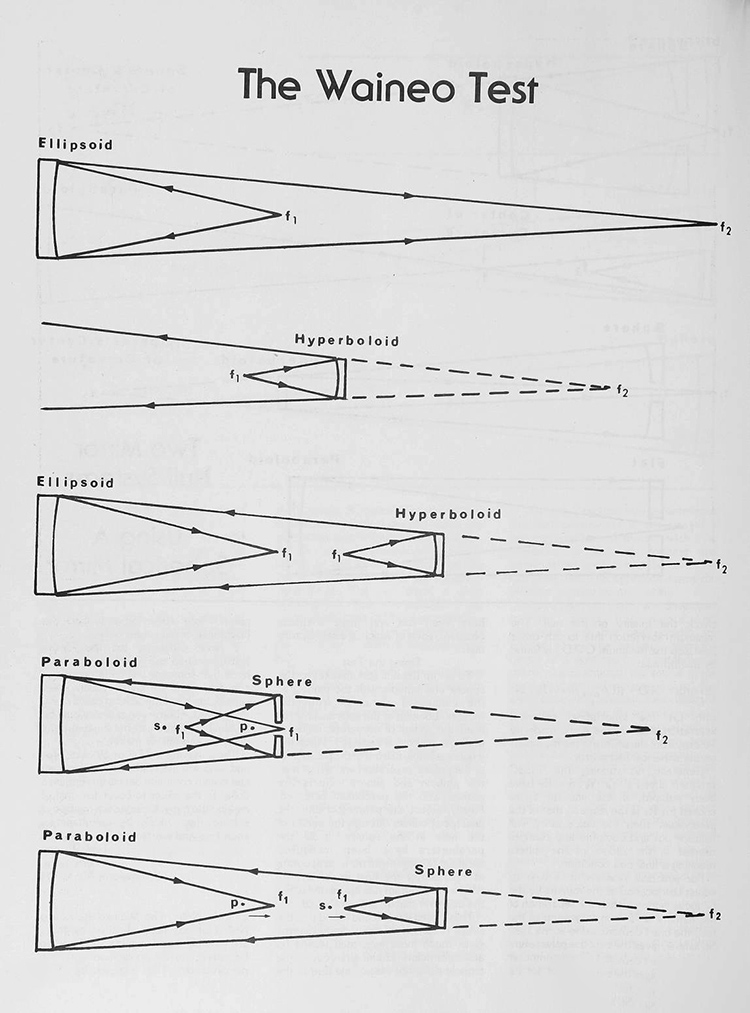
Telescope Making No11 1981г

Автор: Томас Вайнео

Что такое нуль-тест?

Оптики уже давно используют тест Фуко с ножом-лезвием в центре кривизны зеркала при его проверке. Если каждый из лучей, возвращающихся от зеркала, перекрывается ножом-лезвием, поверхность равномерно темнеет. Для сферы тест Фуко является нуль-тестом. Любое несовершенство на поверхности видно как тень или яркая область — что оптик может оценить и устранить путем соответствующей обработки.

Нуль-тест может быть применен к другим коническим поверхностям. Существует два типа: первый использует геометрические фокусы для создания нуля, другой использует вносимые аберрации, которые уравновешивают аберрации желаемой фигуры для достижения нуля.

Помимо сферы, проверяемой в ее центре кривизны, другие примеры геометрических нуль-тестов включают эллипсоид с источником света в одном фокусе и ножом-лезвием в другом (и снова, когда оптика равномерно темнеет по всей поверхности из-за ножа-лезвия в световом пучке, мы имеем идеальный эллипсоид), и звездный нуль-тест, в котором нож-лезвие перекрывает свет яркой звезды, приходящий в фокус. (Другой фокус параболоида находится бесконечно далеко — у звезды — поэтому, когда зеркало равномерно темнеет по всей поверхности, эта поверхность является параболоидом.) Изменяющиеся температуры и воздушные потоки делают этот метод сложным.

Наиболее известный любительский нуль-тест второго типа — это тест Далла. Для этого теста плоско-выпуклая линза помещается внутри ее фокусного расстояния. Правильно выбранная линза вносит сферическую аберрацию, которая уравновешивает сферическую аберрацию параболоида, проверяемого в его центре кривизны. Одним большим преимуществом является то, что одна линза может проверять большой диапазон зеркал. К сожалению, многие любители не добились успеха в применении этого теста, не потому что он недостаточно точен, а потому что проверочная линза должна быть такой же хорошей или лучше, чем проверяемая поверхность. Помните: никакой нуль-тест не может быть лучше, чем качество вспомогательной оптики, используемой для его проведения.

Если нуль-тест может быть выполнен с использованием линзы, он также может быть применен с использованием зеркальной оптики. Один такой тест описан в книге Optical Shop Testing Д. Малакары, в главе 14. Тесты, представленные в этой книге, показывают нуль-зеркало, размещенное позади центра кривизны проверяемого зеркала, за исключением тестов для вогнутого или выпуклого гиперболоида.

Среди этих тестов тест Хиндла обеспечивает нуль для вторичного зеркала Кассегрена с использованием сферического зеркала (см. TM-1, страницы 10, 12, 13), а для вогнутого сферического зеркала уравновешивает аберрации проверяемого зеркала (Silvertooth test). В обоих этих тестах сферическое зеркало используется с его центром кривизны в одном из фокусов гиперболоида, поэтому проверочное зеркало действует как автоколлимирующий источник, так же как плоское зеркало, используемое при проверке параболоида в его фокусе.

Именно расположение этого последнего теста (с разумным разделением проверочного зеркала и асферического зеркала) привлекло мое внимание. Почему бы не применить этот метод для обработки параболоида вместо гиперболоида? Я рассудил, что если мы сможем применить тест близко к коническому фокусу вместо центра кривизны, у нас будет меньше сферической аберрации для компенсации. Таким образом, сфера с большим радиусом может обеспечить нуль.

Ну, если говорить кратко, тест работает, и он применим к ряду проверочных задач. Хотя в первую очередь предназначен для проверки параболоидов, с небольшими изменениями в расчетах он может быть использован для других конических поверхностей, таких как первичное зеркало Ричи-Кретьена. Это простой способ проверить быстрое, короткое коническое зеркало с соотношением 1/2​ с вспомогательной оптикой известного высокого качества — ведь любой хороший изготовитель зеркал может создать отличное сферическое зеркало для этого нуль-теста!

Как и в случае других нуль-тестов, балансирующих аберрации, перед применением к новым проверочным ситуациям следует определить остаточные аберрации, чтобы найти разности оптического пути в нуль-волновом фронте. Балансировки только аберраций 3-го порядка недостаточно. Однако мы рассчитали остаточные аберрации, и они довольно малы: для параболоида 6" f/4 разность оптического пути 5-го порядка составляет около 1/400 длины волны, а все высшие порядки в сумме дают около 1/300 длины волны. В отражательной оптике нет хроматических аберраций, поэтому можно использовать свет любой длины волны или цвета.

Теория теста

Для функционирования нуль-теста должны быть выполнены следующие условия: (1) Вогнутая коническая поверхность должна сама по себе преобразовывать расходящуюся волну от точечного источника в сходящуюся, хотя и с аберрациями, волну. Величина аберраций должна быть противоположна той, что вносится вогнутой сферой. (2) Аберрации, вносимые конической поверхностью, должны быть низких порядков сферических, а высшие порядки должны быть достаточно малы, чтобы не влиять на желаемое качество нуль-волнового фронта.

В нуль-тесте для сферы, когда источник перемещается внутрь к зеркалу от центра кривизны, зеркало возвращает лучи в фокус за пределами радиуса кривизны. Нож-лезвие не может показать нуль во втором фокусе, так как лучи не передаются между геометрическими фокусами зеркала. Если эту сферическую поверхность изменить на эллипсоид, второй фокус даст нуль. Степень изменения определяется двумя терминами — эксцентриситетом, e, и константой конического сечения, K.

При заданном эксцентриситете фокусы могут быть определены по формулам:

F1=R/(1+e)

F2=R/(1−e)​

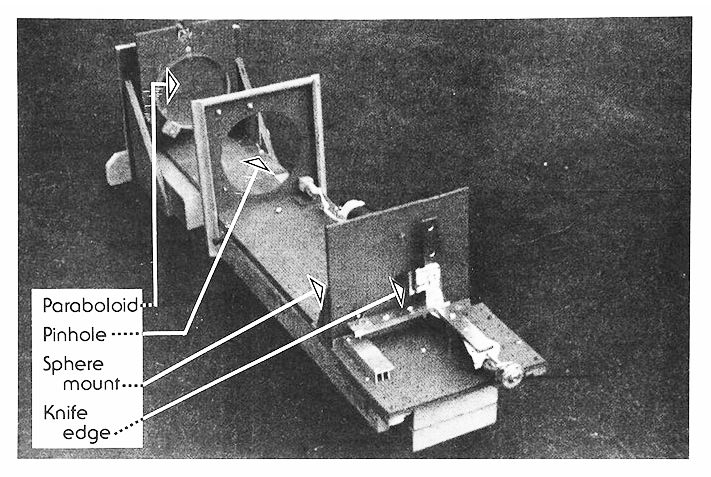
Надписи на фото: Параболоид - Точечное отверстие - Крепление сферы - Нож Фуко

Или если заданы радиус и фокусы, эксцентриситет можно найти по одной из двух формул:

e=(R/F1)−1

e=1−(R/F2)

Константа конического сечения связана с эксцентриситетом соотношениями:

K=−e²

e = (-K)^0.5

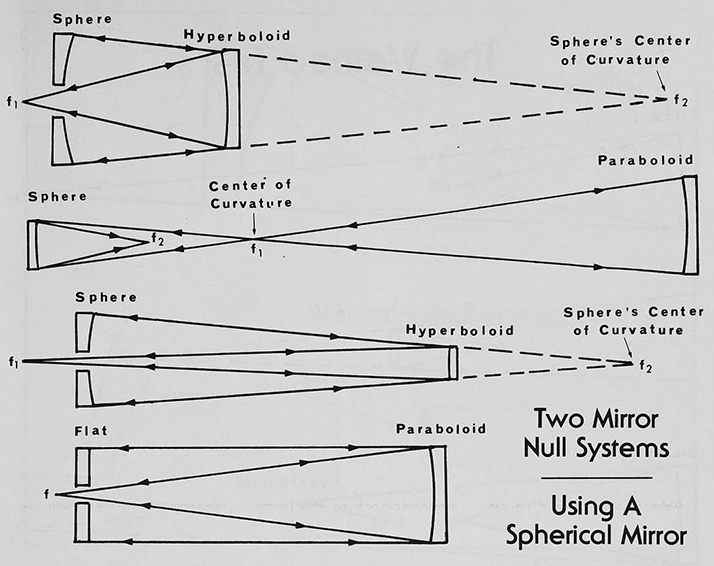
Для сферы e = 0 и K = 0. Для эллипсоида e изменяется от 0 до 1, а K от 0 до -1.

При приближении источника к зеркалу второй фокус быстро удаляется от него. Когда источник достигает половины радиуса зеркала, подвижный фокус уходит на бесконечность. Если зеркало даёт нуль, e = 1 и K = −1. Кривая становится параболоидом, а второй фокус лежит на бесконечности. Плоское зеркало может возвращать лучи обратно к источнику в фокусе — это автоколлимационный тест, пример нуль-теста второго типа.

Если переместить источник ещё ближе, эксцентриситет e становится больше 1, а константа K отрицательнее -1. Поверхность теперь гиперболоид, отражающий лучи расходящимся пучком, но если продлить их за зеркало, мы найдём мнимый фокус (в формулах он обозначается отрицательным значением).

Анализ фокусов конических сечений показывает, что нуль-тест можно создать, комбинируя фокусы эллипсоида и гиперболоида. Однако мало кто захочет шлифовать вторую асферическую поверхность для тестирования, даже если нуль-тест поможет её обработать. Можно заменить эллипсоид сферой в автоколлимационном режиме, но тогда получится гиперболоид вместо нужного параболоида. Есть ли способ использовать сферу для нуль-теста параболоида?

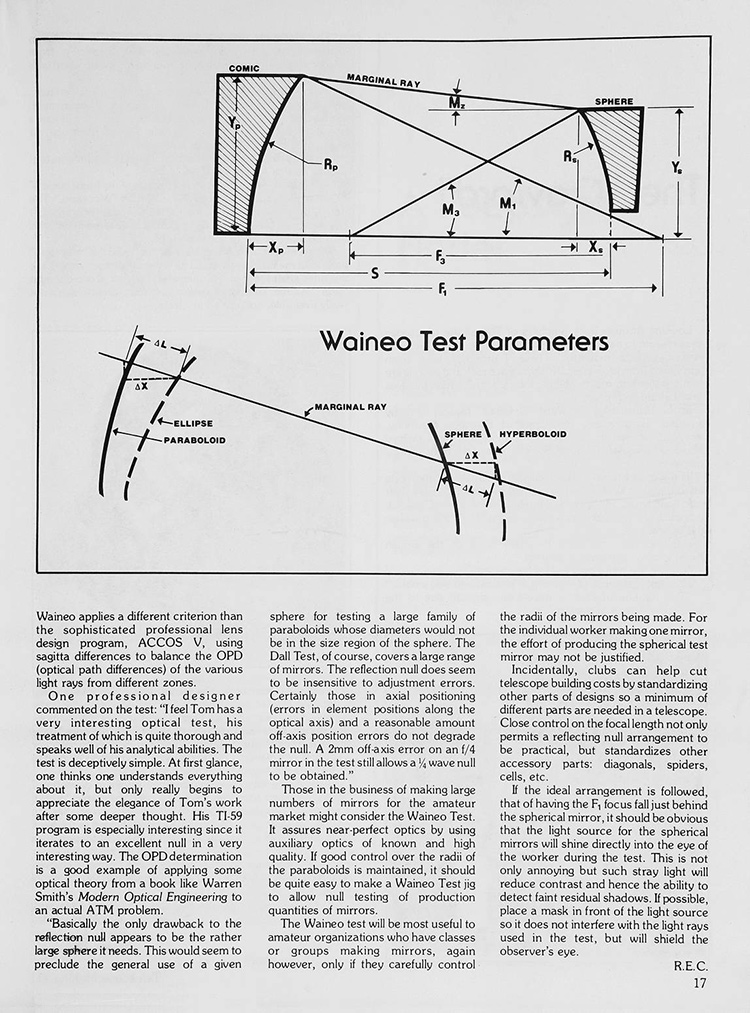
Да, если сохранить геометрическую симметрию гиперболоида и эллипса, но заменить оба зеркала на сферу и параболоид. Без изменения вершинных радиусов параксиальные фокусы останутся прежними.

Теперь параболическое зеркало имеет сферическую аберрацию в фокусе F2, так как работает в эллиптическом режиме, а сфера вносит аберрацию, имитируя гиперболоид. Задача — сбалансировать их.

Идеального баланса для всех лучей достичь невозможно, но можно приблизиться. Если выровнять фокусы параксиальных (центральных) и маргинальных (крайних) лучей, мы скорректируем сферическую аберрацию 3-го порядка. Остаточные аберрации высших порядков останутся, но будут малы.

Как сбалансировать сферу?

1. Изменить её радиус до совпадения лучей.

2. Переместить сферу без изменения радиуса.
   (Программа перемещала 5-дюймовую сферу для теста 6" f/4 параболоида 34 раза на суммарные 12.7", уменьшила её диаметр до 4.3", последняя коррекция составила 0.00029").

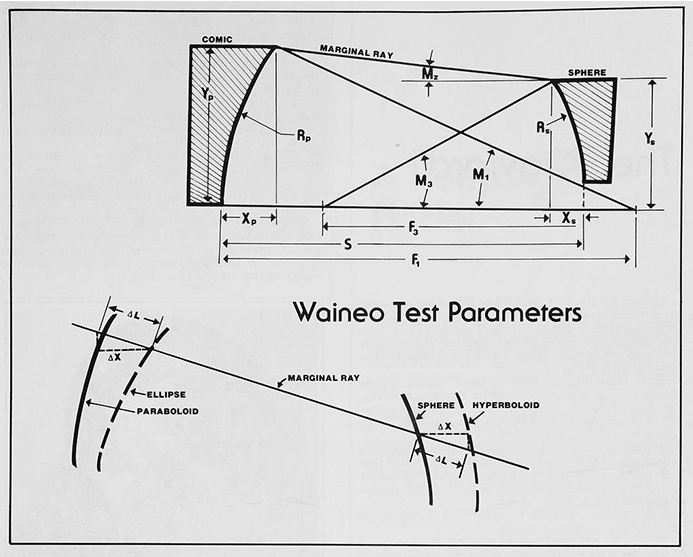
После расчётов нужно проверить применимость системы:

• Если оба фокуса между зеркалами — потребуется диагональ для вывода лучей.

• Если фокус конического зеркала за сферой — можно перфорировать сферу.

• Фокус сферы должен быть удобен для размещения источника света. В противном случае придётся менять радиус сферы.

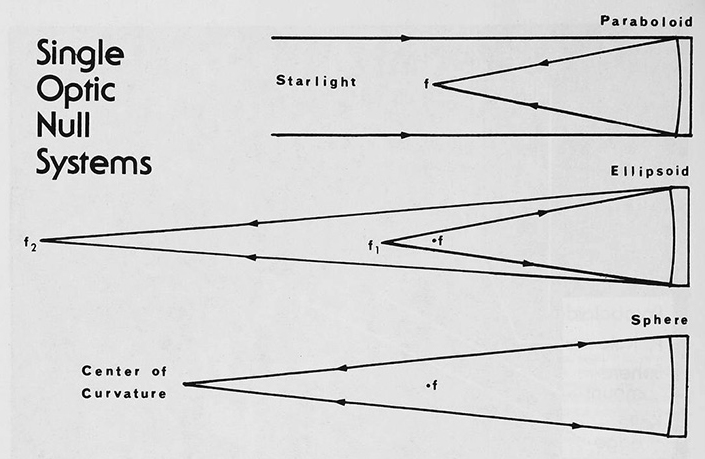
Одноэлементные нуль-системы

Надписи на рисунке: Звездный свет - Эллипсоид - Сфера - Центр кривизны

...при этом фокус оказывается позади тестируемого зеркала, что нежелательно для перфорации. Мы в хорошем положении, если можем рассчитать сферу диаметром от 3/4 до 3/4 диаметра конического зеркала и в пределах 30% от его радиуса. Практичная нуль-система имеет F2​  в 15–50 раз больше диаметра конического зеркала.

Расчёт нуль-системы

Для вычислений необходимы:

• F2​  — параксиальный фокус,

• Yp​  — полудлина параболоида,

• Rp​  — радиус параболоида,

• Ys​ или Rs​  — полудлина или радиус сферы.

Для каждого значения F2​ существует бесконечное количество решений.

Примерное расстояние между зеркалами:

(Точное значение определяется трассировкой лучей.)

Фокус F1​  находится по формуле эллипса или уравнению объект-изображение:

Процедура:

1. Определить первый луч, соединяющий точку на параболоиде с фокусом F1​ .

2. Рассчитать направление луча после отражения.

3. Сбалансировать аберрации через разницу саггит (глубин поверхности).

4. Продолжить трассировку. Если разница между маргинальным и параксиальным фокусами (ΔFi​ ) превышает 0.000001 дюйма, скорректировать радиус или размер сферы.

Ключевые моменты:

• Отклонения поверхности измеряются вдоль нормали к волновому фронту.

• Для упрощения можно использовать маргинальный луч. Если ΔL (расстояние от центра сферы до F2​ ) и ΔX (разница саггит) равны, баланс достигнут.

Программный расчёт

Автор разработал программу для калькулятора Texas Instruments 58C, требующую пяти входных параметров:

1. Высота луча на параболоиде (Yp),

2. Радиус параболоида (Rp​),

3. Расстояние F2​ ,

4. Высота луча на сфере (Ys) или её радиус (Rs​),

5. Начальное приближение для переменного параметра.

Результаты:

• Программа выводит данные нуль-системы (или их можно извлечь из памяти калькулятора).

• Время расчёта: 2–5 минут (зависит от близости начальных параметров к решению).

Проверка нуля

Достаточно балансировки аберраций 3-го порядка. Максимальная продольная сферическая аберрация возникает в зоне ~70% радиуса параболоида.

Надписи на картинке: Сфера - Гиперболоид - Центр кривизны сферы - Сфера - Центр кривизны - Центр кривизны сферы - Сфера - Гиперболоид - Плоскость- Параболоид

Проверка качества нуля

Минимальная аберрация 5-го порядка (и минимальная оптическая разность хода, OPD) вычисляется по формуле:

где:

• LAmax⁡​  — максимальная продольная сферическая аберрация,

• U3​  — угол между лучом от источника и высотой луча на сферическом тестовом зеркале.

Работа с программой T158C

После ввода параметров F2, Yp, Ys, и Rp, если начальное значение Rs​  совпадает с радиусом параболоида, программа автоматически сбалансирует систему и вычислит необходимые изменения радиуса сферы для достижения нулевого условия.

Практические рекомендации:

• Лучше расположить зеркала так, чтобы фокус F1​  был больше расстояния между зеркалами S.

• Такая конфигурация, продемонстрированная на Stellafane в 1980 году, обеспечивает оптимальные параметры (они записаны на лентах T158).

• Для трёх разных положений F2​  были получены три удовлетворительных нуль-решения.

Настройка теста:

1. Установите сферу и точечное отверстие на рассчитанных расстояниях.

2. Отцентрируйте сферу, наблюдая её из центра кривизны.

3. Разместите систему перед параболоидом с правильным разделением и отцентрируйте её.

4. Настройте параболоид так, чтобы конечный фокус проходил через отверстие в сфере.

Если все параметры измерены точно (достаточно рулетки), итоговое изображение окажется в расчётной точке, подтверждая, что зеркало — параболоид.

Преимущества метода:

• Одиночное отражение от непокрытого зеркала даёт больше света, чем автоколлимация.

• Яркость возвращаемого пучка делает наблюдение через точечное отверстие комфортным.

Программное обеспечение:

Автор разработал программы для калькуляторов Texas Instruments 58 и 59. Он предлагает перевести формулы для Hewlett-Packard и приветствует создание версий для домашних компьютеров.

Контакты:

Tom Waineo
6 Perham St., Chelmsford, MA 01824
(Отправьте $1 для получения подробностей, включая метод расчёта OPD через системы уравнений и интегрирование.)

Примечание редактора:

Тест Вайнео был проверен тремя профессиональными оптиками-разработчиками и признан корректным в применении и результатах.

Особенности теста Вайнео

В отличие от профессиональной программы проектирования линз ACCOS V, Вайнео использует разницу саггит (глубин поверхности) для балансировки оптической разности хода (OPD) лучей из разных зон зеркала.

Отзыв профессионала:

"Тест Тома представляет значительный интерес. Его подход тщательно проработан и демонстрирует выдающиеся аналитические способности. Метод обманчиво прост — на первый взгляд кажется понятным, но истинная элегантность решения раскрывается только при глубоком изучении. Его программа для TI-59 особенно впечатляет, так как итеративно достигает превосходного нуля уникальным способом. Метод расчёта OPD — отличный пример применения теории из книг вроде "Современной оптической инженерии" Уоррена Смита к реальным задачам любителей телескопостроения."

Ограничения метода:

• Требуется крупная сфера, что ограничивает её применение для тестирования параболоидов разного диаметра (в отличие от теста Далла, охватывающего широкий диапазон).

• Однако тест устойчив к ошибкам юстировки:

  • Осевые смещения до 2 мм для зеркала f/4 сохраняют точность нуля в пределах ¼ длины волны.

Практическое применение:

1. Для производителей зеркал:

   • Тест гарантирует почти идеальное качество при использовании высококлассной вспомогательной оптики.

   • При контроле радиусов параболоидов можно создать шаблонную оснастку для серийного тестирования.

2. Для любительских клубов:

   • Идеален для группового изготовления зеркал при строгом соблюдении радиусов.

   • Для одиночных проектов создание сферического тестового зеркала может быть нецелесообразным.

Советы по организации:

• Стандартизация фокусных расстояний упрощает не только тестирование, но и производство аксессуаров (диагоналей, держателей и т.д.).

• Защита от засветки: если фокус F1 находится за сферой, источник света может мешать наблюдателю. Рекомендуется использовать маску, блокирующую паразитный свет, но не влияющую на тестовые лучи.

Подпись:

R.E.C.